| 發表文章 | 發起投票 |
[學術討論] A4紙好定B4紙好用?
A系列
A系列紙張尺寸的長寬比都是1:\sqrt{2},然後捨去到最接近的公釐值。A0定義成面積為一平方公尺,寬高比為1:\sqrt{2}的紙張。接下來的A1、A2、A3……等紙張尺寸,其長邊為前一號紙張的寬邊,並在面積最接近但不超過標準值的情況下,盡可能的將寬邊取整為最大的公釐值。要注意的是,寬邊並不單純等於前一號紙張的長邊之半,或是當前紙張長邊除以\sqrt{2}。(例如A1按照四捨五入計算其寬邊應為595公釐,但如此一來面積將超過0.5平方公尺,故為594公釐)。最常用到的紙張尺寸是A4,它的大小是210乘以297公釐。依定義可推出An紙張寬度為2^{-1/4-n/2}米,長度為2^{1/4-n/2}米,面積為2^{-n}平方米。
B系列
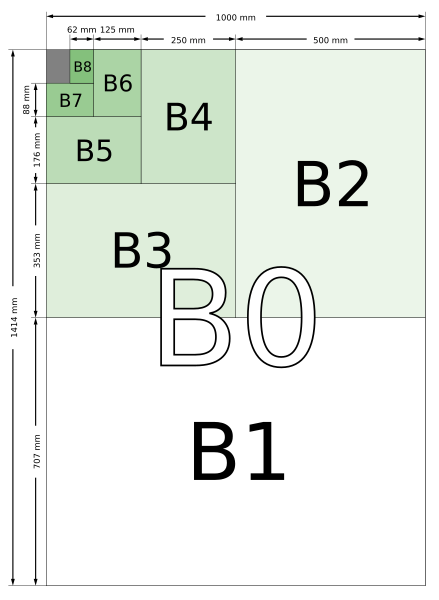
B系列紙張尺寸是編號相同與編號前一號的A系列紙張的幾何平均。舉例來說,B1是A1和A0的幾何平均。同樣地,C系列紙張尺寸是編號相同的A、B系列紙張的幾何平均。舉例來說,C2是B2和A2的幾何平均。此外,日本有一種不相容的B系列紙張尺寸,是用算術平均而不是用幾何平均來定義的。依定義可推出Bn紙張寬度為2^{-n/2}米,長度為2^{1/2-n/2}米,面積為2^{1/2-n}平方米。
C系列
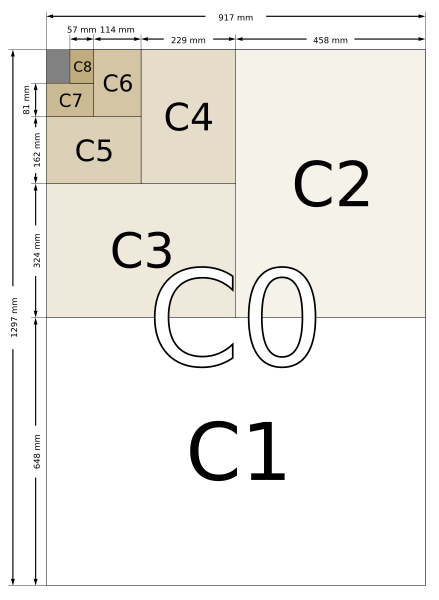
[#ff0011]C系列紙張尺寸主要使用於信封。[/#ff0011]一張A4大小的紙張可以剛好放進一個C4大小的信封;把A4紙張對摺成A5紙張,就可以剛好放進C5大小的信封,餘此類推。依定義可推出Cn紙張寬度為2^{-1/8-n/2}米,長度為2^{3/8-n/2}米,面積為2^{1/4-n}平方米。
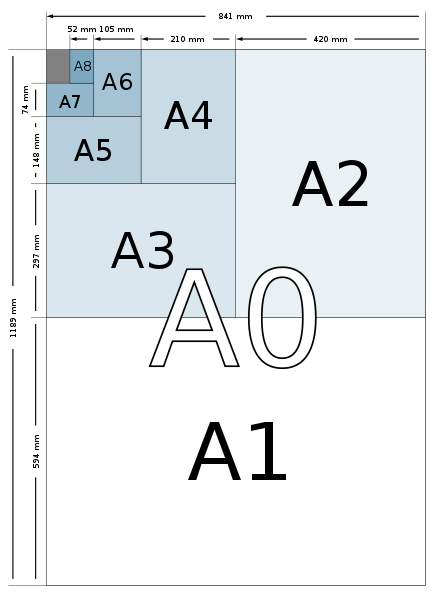
A系列紙張尺寸的長寬比都是1:\sqrt{2},然後捨去到最接近的公釐值。A0定義成面積為一平方公尺,寬高比為1:\sqrt{2}的紙張。接下來的A1、A2、A3……等紙張尺寸,其長邊為前一號紙張的寬邊,並在面積最接近但不超過標準值的情況下,盡可能的將寬邊取整為最大的公釐值。要注意的是,寬邊並不單純等於前一號紙張的長邊之半,或是當前紙張長邊除以\sqrt{2}。(例如A1按照四捨五入計算其寬邊應為595公釐,但如此一來面積將超過0.5平方公尺,故為594公釐)。最常用到的紙張尺寸是A4,它的大小是210乘以297公釐。依定義可推出An紙張寬度為2^{-1/4-n/2}米,長度為2^{1/4-n/2}米,面積為2^{-n}平方米。
B系列
B系列紙張尺寸是編號相同與編號前一號的A系列紙張的幾何平均。舉例來說,B1是A1和A0的幾何平均。同樣地,C系列紙張尺寸是編號相同的A、B系列紙張的幾何平均。舉例來說,C2是B2和A2的幾何平均。此外,日本有一種不相容的B系列紙張尺寸,是用算術平均而不是用幾何平均來定義的。依定義可推出Bn紙張寬度為2^{-n/2}米,長度為2^{1/2-n/2}米,面積為2^{1/2-n}平方米。
C系列
[#ff0011]C系列紙張尺寸主要使用於信封。[/#ff0011]一張A4大小的紙張可以剛好放進一個C4大小的信封;把A4紙張對摺成A5紙張,就可以剛好放進C5大小的信封,餘此類推。依定義可推出Cn紙張寬度為2^{-1/8-n/2}米,長度為2^{3/8-n/2}米,面積為2^{1/4-n}平方米。



本貼文共有 0 個回覆
此貼文已鎖,將不接受回覆
| 發表文章 | 發起投票 |

